Сергей Валянский

Что такое хронотроника?

О хронотронике пока мало кто знает. Большинство тех, кто хотя бы слышал о ней, это последователи А.Т. Фоменко и независимые исследователи, короче, сторонники новых подходов к истории. Но и у них наблюдается некий "перекос восприятия": эту науку воспринимают как отдельное от "Новой хронологии" А.Т. Фоменко течение, занимающееся исключительно хронологическими построениями. Но это совсем не так!

Хронотроника: лозунг, стиль мышления, наука

ХРОНОТРОНИКА (искусственное слово, которое значит "создание времени", и под которым понимается реконструкция прошлого и прогноз возможного будущего, с указанием оптимального пути развития на основе методов естественных и гуманитарных наук) – междисциплинарная наука, изучающая эволюцию общества во времени и пространстве, как систему взаимовлияния человека и природы, с целью нахождения оптимальных путей развития в условиях ограниченных ресурсов, на основе выявления объективных закономерностей в природе и обществе.

Термин "хронотроника" можно рассматривать в трёх смыслах. Во-первых, она выступает как лозунг, под которым объединяются усилия разных наук, для описания процессов эволюции сложных динамических систем разной природы.

Во-вторых, под хронотроникой понимается определенный стиль мышления. Как известно, методология науки различает ряд сменяющих друг друга стилей мышления. Это детерминистский стиль мышления, наиболее ясно сформулировал французский учёный П.С. Лаплас (1749-1827). Во второй половине XIX века стал развиваться вероятностный стиль мышления. В 1980-х годах появился "нелинейный" стиль мышления; в рамках разработки этого стиля мышления и работает хронотроника. Она определяет, какие закономерности действуют, и какие виды структур могут иметь место в процессах эволюции.

И, наконец, хронотроника выступает как некая новая наука, предмет изучения которой составляет то общее, что имеется в процессах эволюции в различных динамических ("живых") системах, независимо от их природы. Сами же эти области выступают как сферы её применения. И прежде всего хронотроника занимается описанием эволюционных процессов в социальных системах, а основанием для её существования служит наличие общих принципов, управляющих возникновением в пространстве и времени самоорганизующихся структур и их разрушением. Уточним: хронотроника основана на идеях о целостности мира и научного знания о нём, общности закономерностей развития объектов всех уровней организации материи в природе, обществе, духовном мире.

Своей задачей – помимо изучения эволюции сложных систем – хронотроника видит выработку рекомендаций по наилучшим приёмам и методам воздействия на развивающиеся системы для быстрейшего достижения ими поставленной цели. Если же говорить о её методах, то, находясь на стыке естественных и гуманитарных наук, она использует комплекс теоретических и экспериментальных методов, развитых в этих науках, базируется на достижениях этих наук и, в свою очередь, влияет на их развитие.

К числу дисциплин, составляющих теоретическую основу хронотроники, относятся некоторые разделы математики, теории информации, методы нелинейной физики, результаты наработок в биологии и конкретных гуманитарных науках (психологии, социологии, истории, философии и т.д.). Кроме того, возникнув на базе обобщения и дальнейшего развития методов кибернетики и топологической теории нелинейных динамических систем, она является их наследницей.

Однако следует отметить, что роль хронотроники не сводится только к использованию методик нелинейной физики и математики. Опробование решений хронотронических задач на конкретных примерах из разных наук делает их наглядными и развивает определённую интуицию у человека, освоившего её основы.

По мере развития хронотроники описываемые ею сценарии эволюции сложных систем, содержащие переход от порядка к хаосу и обратно, казавшиеся ранее редкими и случайными, стали с лёгкостью обнаруживаться в окружающем нас мире: оказывается, образование диссипативных структур происходит в различных системах постоянно и непременно. Иначе говоря, если раньше казалось, что переход динамической системы к стохастическому режиму – какая-то экзотика, существующая в специально придуманных системах, каков, например, бильярд Синая, то сейчас видно, что динамические системы гораздо чаще переходят в стохастический режим, чем сохраняют детерминированное поведение. Обнаружение такой закономерности в социальных системах как раз и делает хронотронику популярным лозунгом, а неоднозначность реконструкций как назад по времени (в попытках понять историю), так и вперёд (в попытках смоделировать возможное будущее) и поиск реальных траекторий среди этого множества должно способствовать росту её популярности.

Хронотроника может стать мощным основанием для современных теоретических общественных наук. С её помощью социальные, экономические, исторические и т.п. законы могут приобрести количественную форму, станет возможным делать более точные количественные и качественные предсказания. Суть её подхода заключается в совместном использовании обычного анализа и численных расчётов с помощью современных вычислительных машин для получения ответов на вопросы социального содержания. И это полезно, так как каждый из этих подходов имеет ограниченные возможности при решении нелинейных задач. При этом должно быть понятно, что хронотроника вынуждена создавать свою специфическую терминологию и язык, потому что она должна соединить представления математики с понятиями тех наук, к которым они будут применяться.

Краткий анализ понятия "хронотроника", приведённый выше, преследовал одну цель: показать, что под этим понятием скрывается целый спектр различных конкретных реализаций этого понятия, и не различение этих особенностей приводит к путанице, что и показывают, в частности, споры на некоторых интернет-форумах.

Идеи, выдвигаемые хронотроникой, могут не только помочь в понимании эволюционного пути человечества в прошлом (истории), но и быть полезными для более осмысленного движения в будущее, и даже послужить основанием для создания общественных движений. Это важно, поскольку из всех возможных вариантов будущего ныне реализуются не самые лучшие, а для развития лучших надо хотя бы, чтобы они стали известными, понятными, и продемонстрировать свою привлекательность.

Основные принципы построения и исследования системы уравнений для описания эволюции сложных динамических систем

"... В последующие годы я не мог себе простить этот недостаток выдержки,

не позволивший мне одолеть математику хотя бы настолько,

чтобы разобраться в её великих руководящих началах;

у людей, усвоивших эти принципы, одним органом чувств больше,

чем у простых смертных..."

Дарвин Ч. Собрание сочинений М.- Л., 1925, т. 1. кн. 1.

Здесь мы попробуем объяснить не математикам, как работает математический аппарат, который предлагается использовать для решения задач, возникающих в гуманитарных науках.

Прежде всего, мы предлагаем классифицировать эти задачи не по принципу описываемого ими явления, а по форме используемых закономерностей, с выведением соответствующих уравнений. А что наиболее, может быть, важно, так это то, что объекты общественных наук всегда эволюционируют в условиях ограниченных ресурсов. А это значит, что уравнения, описывающие их поведение, являются принципиально нелинейными!

Эволюционный процесс любой динамической системы, в том числе человеческих сообществ, математически можно описывать векторным полем скоростей изменений параметров в фазовом пространстве. Под фазовым пространством мы будем понимать пространство, образуемое основными параметрами, определяющими поведение системы, и скоростями их изменений. Точка фазового пространства задаёт состояние системы.

Последовательность точек в фазовом пространстве, описывающая эволюцию системы, называются фазовыми кривыми. В некоторых точках вектор скорости может обращаться в нуль. Такие точки называются положениями равновесия (тут состояние не меняется с течением времени). Периодические процессы изображаются замкнутой кривой на фазовой плоскости; эта кривая называется предельным циклом.

Системы, описывающие реальные эволюционные процессы, всегда зависят от разных параметров, которые никогда не бывают известными точно. Поэтому малое общее изменение параметров превращает систему необщего положения в систему общего положения, что действует для всех случаев, кроме некоторых исключительных.

Исследуемая система уравнений имеет вид:

,

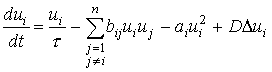где a_i < b_ij, i ≠ j, u_i – концентрация элементов i-го типа, т.е. в каждом элементе уже сделан выбор одного из вариантов. (1/τ)u_i описывает автокаталитическое воспроизводство; b_i,ju_iu_j – описывает взаимодействие элементов – со знаком минус, т.к. взаимодействие носит антагонистический (конкурентный) характер); a_iu_i²– описывает эффект тесноты (гибель при встрече двух одинаковых элементов, этот член становится существенным при большой концентрации одинаковых элементов; D – коэффициент миграции через границу.

В рамках этой модели можно:

А) Провести описание распределённых систем, найти однородные стационарные решения и провести анализ на их устойчивость.

Б) Дать качественный анализ характера распространения возмущений, синхронизации автоколебаний в пространстве и образования структур.

В) Выявить условия существования режимов с обострением и солитонные решения.

Безусловно, все процессы в социальных системах разворачиваются как во времени, так и в пространстве. Поэтому наиболее адекватные модели этих процессов описываются системами уравнений в частных производных. Однако в очень большом числе случаев можно считать, что во всех частях рассматриваемого объёма процессы синхронны и, следовательно, зависимость от координат отсутствует. Это даёт возможность в большинстве случаев перейти к более простой системе обыкновенных дифференциальных уравнений:

dx_i /dt =F_i(x₁, x₂, ..., х_n) (i = 1, 2, ..., n). (1)

Величины F_i(x₁, x₂, ..., х_n)– нелинейные функции определяющих эволюцию системы переменных х_i (не зависящих явно от времени t); обычно они состоят из нескольких слагаемых, описывающих баланс разных факторов, влияющих на эволюционную систему. Положительные члены описывают прибыль компонента х_i , отрицательные – убыль. Для построения системы достаточно знать скорости притока и оттока каждого компонента и их зависимость от переменных х_i.

Модели типа (1) хорошо известны и широко применяются при решении задач химической и биологической кинетики. Можно пользоваться результатами, полученными в этих областях, указав лишь некоторые различия, присущие задачам "социальной кинетики".

1. В исследованиях по общественным наукам, в зависимости от задачи, используются различные переменные. Например, в экономике – это денежные, товарные или энергетические потоки; в социологии – численность различных социальных групп; в экологии – количество ресурсов и т.п.

2. Очень часто процессы, идущие в социальных системах, разбиваются на ряд элементарных стадий, скорости которых зависят от динамических переменных достаточно просто, т.е. нелинейные функции F_i(x₁, x₂, ..., х_n) представимы в виде полиномов сравнительно низкой степени. Степень полинома в уравнении совпадает с порядком процесса.

3. В общественных науках при описании различных процессов часто идут процессы авторепродукции (эквивалентные тем, что наблюдаются в биологических процессах).

4. Пространственная неоднородность и связанные с нею эффекты играют в ряде социальных процессов значительную роль, так как большинство этих процессов локализовано в определённых участках пространства, которые отделены друг от друга определёнными же границами. Эта гетерогенность пространства, разделение его на природные "кластеры", имеет очень важное, а зачастую и основное значение.

5. В общественных науках число участвующих в социальных процессах объектов может быть достаточно малым, даже порядка единицы. При этом в качестве динамических переменных удобнее использовать вероятность застать объект в том или ином состоянии.

6. Часто высказывается мнение, что процессы, изучаемые общественными науками, много сложнее, например, биологических. Это, несомненно, так. Но мы не достигли бы успеха и в процессах, изучаемых естественными науками, если бы не знали, как выделить основное в них, не обращая внимание на второстепенное. Критерием простоты является не число элементарных стадий в рассматриваемом процессе, а возможность эффективного упрощения исходной системы, уменьшения числа уравнений и числа динамических переменных. В этом смысле социальные процессы даже более просты, чем процессы, изучаемые естественными науками.

Чем же вызвана сложность применения математических методов к задачам гуманитарных наук? Во-первых, почти все системы и процессы, являющиеся предметом изучения этих наук, нелинейны, и вследствие этого, как правило, неустойчивы. Во-вторых,при поиске общих закономерностей всегда есть опасность ввиду большой разнородности и своеобразия приложений быть сбитыми с толку техническими деталями, возникающими при решении отдельных задач. И, в-третьих, в самих этих науках нет понимания, какие процессы следует понимать как определяющие, а какие как второстепенные, и это вносит дополнительную сложность применения математики.

Всё это делает, казалось бы, задачу применения математики к общественным наукам невыполнимой. Но как раз то, что эти задачи, как правило, нелинейные, делает эту задачу вполне разрешимой. Задачу следует упростить до того, чтобы она содержала минимальное число переменных и параметров, чтобы она была "грубой", без излишних шумов, затеняющих закономерность. Как и за счёт чего это может быть сделано?

В процессе функционирования и развития нелинейных систем возникают иерархии масштабов и времени. Благодаря этому возможно определённое упрощение при описании системы, сведение её математической модели к малому числу параметров порядка. Это позволяет применить здесь метод редукции – сведение системы, содержащей большое число дифференциальных уравнений (и, следовательно, переменных) к более простой системе из меньшего числа уравнений. Редуцированную систему уравнений называют базовой. От неё требуется, во-первых,чтобы она описывала основные черты рассматриваемого явления, во-вторых, чтобы она содержала минимальное число переменных и параметров, и, в-третьих, чтобы она была "грубой" в смысле Андронова. Последнее означает, что при малом изменении параметров и слабом расширении базовой системы (то есть добавлении высших производных и/или новых членов с малыми коэффициентами), решения должны меняться мало.

А это, в свою очередь, значит, что на самом деле важен не конкретный вид уравнения, а типы решений, которые могут в нём содержаться, их определённая типология. То есть важна классификация решений.

Кроме того, мы не просто ставим задачу выяснения характера эволюции социальных систем, но и – что не менее важно – желаем научиться управлять такими сложными системами. И действительно, возможно создание таких специальных условий, при которых осуществим перевод изучаемой системы в наперёд заданные параметры.

Как уже сказано, хронотроника основана на идеях целостности мира, общности закономерностей развития объектов всех уровней организации материи, т.е. основанием для её существования служит наличие общих принципов, управляющих возникновением в пространстве и времени самоорганизующихся структур и их развалом; существование переходно-неустойчивых, фрактально усложняющихся процессов; взаимосвязи многовариантности и необратимости, случайности и необходимости.

Этого достаточно, чтобы быть противниками громоздких моделей, содержащих десятки дифференциальных уравнений. Мы глубоко убеждены, что такие модели не помогают, а, скорее, мешают в понимании исследуемых явлений. Модели должны быть простыми, "минимальными" для данной конкретной задачи и, конечно, не могут служить во всех возможных ситуациях.

Очевидна польза "обезразмеривания" (т.е. приведения всех переменных к одному масштабу); это позволяет выявить малые параметры и оценить вклад различных членов в исследуемые процессы.

Существенной помощью в упрощении исходной системы уравнений и сведение её к базовой является следующие методы. Во-первых, это теорема Тихонова [1]. Её смысл заключается в том, что среди различных параметров, описывающих систему, существует временная иерархия. А это позволяет рассматривать не всю систему уравнений, а лишь малую часть, считая большую часть параметров постоянными, так как "быстрые" переменные уже успевают выйти на предельные значения, а "медленные" ещё не успели сильно измениться.

А сделать выбор, какие параметры настолько важны, что их поведение "контролирует" всю систему, можно на основе принципа лимитирующего фактора и принципа Кулона [2].

Переход от порядка к хаосу и от хаоса к порядку, от структуры одной размерности к другой – всё это качественные переходы системы в процессе эволюции. Поэтому хронотроника, на первом (текущем) этапе своего развития выступает как качественная теория. (Здесь понятие "качественное" понимается не только, как появление новых качеств, но и в том смысле, что хронотроника даёт лишь качественные результаты, так как точные численные расчёты очень часто просто бессмысленны). Она может послужить основанием для развития так называемой диалектической логики, позволяя определить границы применимости формальной логики.

Нелинейные уравнения обладают значительной общностью, поскольку в природе существует всего несколько универсальных сценариев перехода от порядка к хаосу и обратно. Можно изучать самые разные явления, писать разные уравнения, а получать одни и те же сценарии. Похоже, в этом проявляется новый, более глубокий уровень единства природы: порядок неотделим от хаоса, а хаос порой выглядит как сверхсложная упорядоченность. Причём часто хаос выступает как признак правильного функционирования сложной системы, а излишняя упорядоченность – как симптом её разрушения.

При изучении нелинейных систем исследователя чаще всего интересуют времена эволюции неустойчивых систем, а не вопрос времени развития соответствующих неустойчивостей. То есть кажется важным время прихода системы, в конце концов, к некоторому предельному состоянию. А оно, как правило, есть сложное положение равновесия между А) флуктуациями в системе, и Б) средними характеристиками, определяющими её макроскопическое состояние, то есть осреднёнными на достаточно большом временном интервале.

Предельное состояние часто обладает либо притягивающими свойствами, тогда, в простейшем случае, оно называется аттрактором, либо, в более общем случае, выступает совокупностью ограничительных для поведения системы свойств в поле данных возмущений. Причём притягивающие свойства, в последнем случае, проявляются лишь после расчёта некоторых средних параметров, определяемых на фазовой траектории системы. Существенно, что предельное состояние часто уже не зависит от ряда деталей начальных условий, важных именно для начального этапа развития системы. Но предельное состояние, находясь под действием поля внешних возмущений, само претерпевает эволюционные изменения.

Сегодня физики уже знают основной "нелинейный" урок, заключающийся в том, что обычно нелинейные уравнения нужно исследовать, не прибегая к привычной процедуре линеаризации, потому что на этом пути нельзя получить ни в каком конечном порядке теории возмущений фундаментальных решений, появляющихся в подобного типа уравнениях.

На сегодняшний день разработан целый ряд руководящих нелинейных концепций, позволяющих безошибочно разбираться в большом классе нелинейных явлений. Повторим, что главная из них – построение и исследование простейших или базовых моделей, описывающих суть явления и позволяющих получить достаточно общие качественные результаты. Их можно описать с помощью базовых уравнений – простейших уравнений, на основании которых можно обнаружить особенности поведения описываемых ими систем. Это позволяет с меньшей затратой сил исследовать более сложные особенности. Например, мы можем плохо знать детали промежуточных процессов и их параметров, но сама возможность колебательного режима легко устанавливается из анализа упрощённых математических моделей.

Кроме того, наибольшую практическую ценность имеют в большинстве случаев именно исследования самых простых и часто встречающихся особенностей. А затрата сил на преодоление технических трудностей, стоящих на пути исследования более сложных случаев, не всегда оправдывается практической ценностью получаемых результатов.

По словам академика В.И. Арнольда, все сложные случаи очень редки в природе и поэтому на первом этапе их можно и не рассматривать. Эта точка зрения обесценивает большую часть теории дифференциальных уравнений и вообще математического анализа, где традиционно основное внимание уделяется малоценным, но трудным для исследования случаям не общего положения [3].

Кроме того, следует учитывать стратегию постепенного усложнения рассматриваемых систем, предлагаемую теорией катастроф. Иначе говоря, вначале следует изучать случаи общего положения, затем вырождения коразмерности один, затем – два, и т.д. То есть, чтобы понять очень сложный процесс, следует выбрать очень простую систему, поведение которой качественно напоминает поведение изучаемой, затем подробно изучить свойства такой упрощённой системы. Это позволит отыскать те "универсальные" характеристики поведения простых систем, которые, видимо, не зависят от конкретных деталей модели. Наконец, эти общие выводы применимы для анализа поведения гораздо более сложных систем.

Простые модели и теории можно применять к сложным нелинейным системам ещё и потому, что нелинейные системы подвержены процессам самоорганизации. Сложные системы имеют очень много степеней свободы, однако всё устроено так, что в процессе эволюции выделяется несколько главных, к которым подстраиваются остальные. Эти главные степени свободы называют "параметрами порядка", и если их немного, есть шанс описать сложную систему просто. Возникает иерархическая структура управления и взаимосвязей.

Конечно, далеко не всякую нелинейную систему можно проанализировать аналитически "вручную", но с помощью компьютера это сделать можно. Компьютерные методы с их ошибками округления, внося фон возмущений в расчёт, являются идеальным средством для исследования динамики неустойчивых систем.

При анализе уравнения (1) особое внимание надо уделять проблемам бифуркации фазовых траекторий, рассматривая связь с теорией катастроф, анализируя поведение особой фазовой траектории – странного аттрактора, учитывая дробную размерность фазовых траекторий – фракталов, наконец, анализируя связь между структурами, хаосом и симметрией процессов.

А особый интерес представляет рассмотрение достаточно простого, но вместе с тем имеющего достаточно большую область применения "логистического" уравнения, а также системы "логистических" уравнений. (Мы берём здесь название "логистическое" в кавычки, так как это не обычное дифференциальное уравнение, а уравнение в конечных разностях, по виду похожее на логистическое.). Анализ подобных уравнений позволяет вырабатывать принципы управления нелинейными неустойчивыми системами.

Незавершённость Истории

Когда молодой Макс Планк выбирал специальность и решил стать физиком, некий друг семьи, профессор, сказал, что он делает большую ошибку, ведь физика в основном завершена. В ней осталось только два лёгких облачка, заявил он, одно из которых – излучение чёрного тела. К счастью, Планк не послушался старого профессора, занялся проблемами излучения чёрного тела и в 1900 году создал новую, квантовую физику.

История науки знает много всяческих "завершителей". Один из самых известных – Аристотель, чье прозвище как раз и означает "Всеобщий Завершитель". А разве на самом деле не развивались науки после него? Поставил ли последнюю точку в биологии Дарвин? Закончилась ли химия на Д.И. Менделееве?

Наука История тоже далеко ещё не завершена.

Нужно понять и принять как данность, что история человечества, как и развитие всей вообще природы и всего мироздания, подчинена объективным законам. История отличается лишь тем, что действие этих законов выражается в ней через деятельность людей, а значит, они (законы) могут проявляться или нет. Например, если мы подойдем к краю пропасти и прыгнем с её края, то под действием объективного закона гравитации мы разобьёмся, когда достигнем её дна. Но мы можем, дойдя до края пропасти, развернуться и уйти от неё. Закон гравитации никуда не исчезает, просто человек, понимая последствия своего поступка, избирает другой путь. Аналогичный общественный закон: революция (падение в пропасть) неизбежна, если доходы десяти процентов самых бедных членов общества в 30 раз меньше, чем у десяти процентов самых богатых. В такой ситуации общество становится абсолютно нестабильным, жди взрыва. Но ведь можно не доводить до крайности, регулируя соотношение доходов, например, через усиленное налогообложение богатых.

Таких законов достаточно много, и если традиционная история не показывает их действия, значит, она неверна и требует пересмотра.

Исполнилось уже почти сто лет новой версии исторической хронологии, предложенной Н.А. Морозовым и дополненной многими его последователями. И что же? Историки-традиционалисты не допускают ревизии в столь милой их сердцу, привычной и уютной науке. Как было написано основателями хронологии Скалигером и Петавиусом в XVI веке, так и есть. Неважно, что за четыреста лет все науки развивались и менялись кардинально; хронология пересмотру не подлежит.

Профессор А.А. Любищев (1890–1972), посвятивший свою жизнь математизации биологии, исследованиям в области прикладной энтомологии, систематики, морфологии и эволюции, говорил, что хотя объём фактов, собранных Н.А. Морозовым, можно сравнить с горой Монблан, всё же фактов традиционной истории хватит на Гималаи. Вопрос в том, как смотреть на эти факты. Ведь история вроде мозаики, или, лучше, калейдоскопа. Смотришь на традиционную пеструю картину и радуешься, как всё красиво и соразмеренно. Однако, повернешь трубочку этого "калейдоскопа", и вдруг получаешь картинку ничуть не менее красивую, но более осмысленную.

Что же теперь делать с историей, как собрать новую мозаику ее фактов?

К сожалению, сегодня история – наука политическая. Задача состоит в том, чтобы сделать её наукой, объективно описывающей прошлое. А социальные процессы в своём развитии подчиняются объективным законам. Вот их нахождение и должно стать предметом истории! На этом пути идеи хронотроники могут стать весьма полезными.

Требуется не только учёт действия этих законов, но и переосмысление на их основе "исторических фактов": не выкидывая их из традиционной истории, мы предлагаем найти им новое место. Нужно по-новому прочитывать старые рукописи. Делать переводы разноязыких летописей и сравнивать их, выявляя в них объективную часть. Применять разнообразные методы: астрономический, географические, этно-психологический, лингвистический и т.д. Надо применять и математику – но не в качестве обоснования хронологических расчётов, а как аппарат, позволяющий дать оценку направлению движения динамических систем.

Сегодня идея пересмотра "официальной" истории уже не достояние элитной группы; любой человек может участвовать в работе. Нужно привлекать энтузиастов; объединять их на местах. Нужно вдумчиво, серьёзно, без погони за сенсациями создавать новую, реальную историю, основанную на разуме.

Только так человечество обретёт разумное настоящее и будущее.

Литература:

1. Тихонов А.Н. //Математический сборник. –1952. – Т. 31.

2. Валянский С.И. Теория информации и образование. Условие выживания России. – М.: АИРО-ХХI; "Крафт+". 2005. – 140 с.

3. Арнольд В.И. Обыкновенные дифференциальные уравнения. – М.: Наука, 1971.