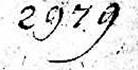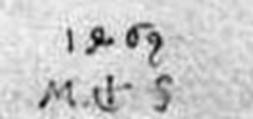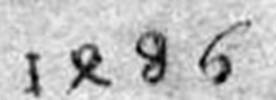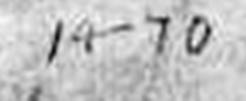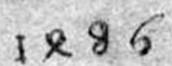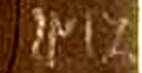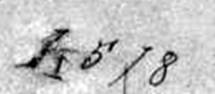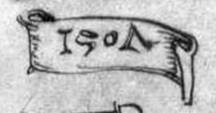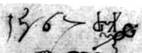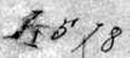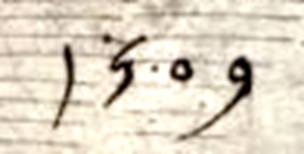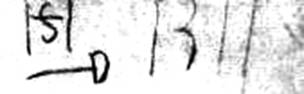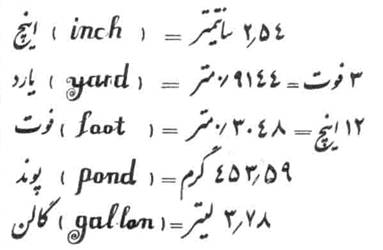Рейтинг: 5 / 5

Владимир Вишнев

Странные даты

Выдержки из коллекции изображений цифр на картинах, гравюрах и рисунках художников XIV – XVII веков.

Гипотеза А.Т. Фоменко и Г.В. Носовского

о происхождении арабских цифр.

Древнерусский бог Семаргл и цифра "семь"

"Странные" цифры на картинах художников

Эволюция арабских цифр в средневековой Европе

О системах счисления

Гипотеза А.Т. Фоменко и Г.В. Носовского о происхождении арабских цифр.

Один из разделов Новой хронологии посвящен происхождению современных цифр.

Основная идея А.Т. Фоменко и Г.В. Носовского в том, что современные арабские цифры произошли из славяно-греческих букв-цифр в XV – XVI веках Нашей Эры.

В книге "Новая хронология Руси, Англии и Рима" (М: Издательство "АНВИК", 1999, глава 45) [1] приведены и обоснованы доводы в пользу этой гипотезы.

Сегодня считается, что позиционная система записи чисел была изобретена в Индии "очень давно", затем была заимствована арабами, которые и занесли ее в средневековую Европу. При этом Индия не была завоевана арабами в их восточных походах. Заимствование индийских цифр у индийцев должно было бы произойти сначала их иранскими и китайскими соседями задолго до арабского покорения Ирана. У иранцев могли быть и другие источники математической учености. В двадцатом веке стали известны знаменитые глиняные таблички, найденные на территории Месопотамии и относимые к цивилизации "древних шумеров". На этих табличках имеются примеры использования позиционной системы счисления, позволявшей производить сложные математические расчеты и решать астрономические задачи. Эти математические достижения древних шумеров и древних индийцев были забыты их потомками. Сегодня материальные свидетельства развития математики в Индии, и в Китае либо исчезли, либо еще не найдены. Предшествующие европейским математические трактаты на арабском языке считаются средневековыми, однако большинство из них стали известны в Европе в XVIII – XIX веках, уже после того, как изложенные в них сведения были открыты европейскими учеными в ходе собственных поисков. Например, наполненные астрономическими и календарными вычислениями труды Бируни, относимые к X веку, стали известны в Европе только в XIX веке.

Современная математика стала стремительно развиваться именно в Европе, во второй половине XVI – начале XVII веков, на основе единых для всей Европы "арабских цифр" и позиционной системы счисления. А.Т. Фоменко и Г.В. Носовский делают естественный вывод о том, что и сама позиционная система счисления распространилась в середине XVI века - в Европе, причем сначала среди математиков и вычислителей, а уже затем среди издателей, художников, школьных учителей. В книгах по Новой хронологии приводится немало примеров "странных цифр и дат" на средневековых и более поздних документах, книгах, картинах.

Иногда кажется, что математические символы являются вненациональным научным инструментом, общим и единым для всех стран и народов. Однако, наши "арабские" цифры отличаются от "арабских" цифр в Иране и в Египте. Европейская позиционная система записи цифр от старших разрядов к младшим, слева направо, также не единственная. На Востоке используется также система записи цифр справа – налево. До сих пор, во многих случаях, в основном в быту, используются и непозиционные системы записи чисел.

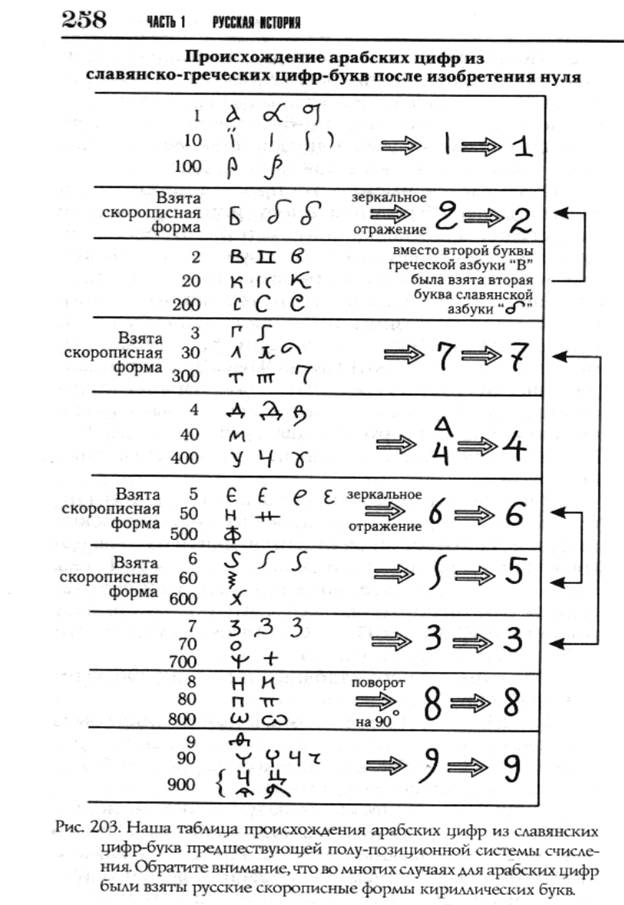
Гипотеза А.Т. Фоменко и Г.В. Носовского о происхождении цифр рассматривается в их книгах. Здесь приведена таблица происхождения арабских цифр из славянских скорописных кириллических цифр-букв [1, 6].

Традиционная история не имеет достаточно обоснованной гипотезы, объясняющей происхождение цифр. В традиционной истории считается, что римская, греческая, египетская системы счисления, в которых цифры записывались словами или образовывались из нескольких значков, предшествовали арабской системе счисления. В середине VIII века НЭ в Багдаде, бывшем в то время культурной и научной столицей мира, где арабские, греческие, персидские, еврейские и другие ученые объединили научные знания своих народов, появились трактаты по астрономии из Индии, содержащие индийскую систему обозначения чисел. В ней цифры, состоявшие ранее из нескольких значков, стали обозначаться одним знаком. Индийский метод давал преимущество в использовании гораздо меньших групп знаков для обозначения числа и значительно упростил письменные вычисления. Если происхождение новой системы было индийским, то, видимо, и изначальная форма арабских числительных также была индийской. Но впоследствии арабские ученые стали использовать собственные обозначения восточно-арабских цифр, которые были образованы, по-видимому, от букв арабского алфавита. В традиционной истории есть предположения об образовании европейских, западно-арабских, цифр как от древних индийских цифр, так и от букв арабского алфавита.

Рассмотрение цифр в датах на картинах, гравюрах, рисунках художников XIV – XVII веков показывает, что до середины XVI века единой для Европы системы написания арабских цифр не существовало. В последней четверти XV века цифры у итальянских мастеров соответствуют современному написанию цифр. Цифры у немецких и голландских мастеров в первой четверти XVI века еще значительно отличаются от современных, разные художники применяют разную форму цифр. Даже при обозначении дат римскими цифрами встречаются разные формы записи чисел, некоторые из них не соответствуют классическим.

Написание цифр на картинах, гравюрах, рисунках художников XIV – XVII веков временами работает на гипотезу А.Т. Фоменко и Г.В. Носовского, временами противоречит их гипотезе. Сомнения в подлинности дат, проставленных на картине, гравюрах и рисунках возникают, однако однозначной уверенности все же нет..

Эволюция арабских цифр в средневековой Европе от X до XV века показана в книге Е.Я. Габовича "История под знаком вопроса" [2], со ссылкой на книгу французского математика марокканского происхождения Дж. Ифрака "Универсальная история чисел" [3]. Там же иллюстрируются метаморфозы цифр "пять" и "шесть" от их древних изображений к современным европейским и иранским. Судя по таблицам Ифрака, к концу XV века в Европе написание цифр соответствует современному, но цифры и даты на картинах художников XVI и даже XVII веков говорят, что это не так.

В данной подборке имеет место несколько спонтанное изложение материала, предлагаемого по мере его нахождения и осмысления. К сожалению, среди довольно большого количества странных цифр и дат не удалось найти "конфетку", которая стала бы открытием для тех кто увлекается Новой хронологией. В произведениях художников странные цифры и даты зачастую соседствуют с вполне нормальными цифрами и датами на картинах, гравюрах и рисунках тех же художников, написанных в том же году. Если расставить иллюстрации соответственно времени создания произведений искусства, нередко после нормальных цифр и дат художник вновь возвращается к странным цифрам. Такое проще всего объяснить тем, что даты в произведениях искусства проставляли несколько человек, возможно, задним числом, с целью подгонки хронологии искусства под традиционную хронологию мировых событий. О том, как исправляли произведения искусства, не только даты, но и сюжеты, особенно на гравюрах, достаточно сведений, причем не только у авторов Новой хронологии.

Таблица из [1]. Гипотеза А.Т. Фоменко и Г.В. Носовского о происхождении арабских цифр.

Древнерусский бог Семаргл и цифра "семь"

В "Повести временных лет" под 6488 (980) годом помещено сообщение о так называемой первой религиозной реформе князя Владимира Святославовича:

"И нача княжити Володимер въ Киеве един, и постави кумиры на холму вне двора теремнаго: Перуна древяна, а главу его сребрену, а ус злат, и Хърса, Дажьбога, и Стрибога и Симаргла, и Мокошь".

Здесь упоминаются важнейшие восточнославянские боги, включенные Владимиром в древнерусский пантеон (спустя 400 лет именно этим богам молился на Куликовом поле хан Мамай). Из этих божеств два являются бесспорно иранскими и, как можно полагать, слабо освоенными русским этническим элементом - Хорс и Симаргл. Хорс был "природным", солнечным божеством, явно неславянского происхождения. "Еще более странно включение Владимиром в этот же ряд Симаргла. Известий о нем в древнерусских источниках практически не сохранилось. Зато имеется прямая аналогия с иранским Сэнмурвом – …речь идет о персидском Симурге, обозначающим сказочную птицу вроде грифа, которая почиталась как божество..., или же о гибридном образе полусобаки-полуптицы. Этот, очень иранский образ, весьма популярный и вместе с тем претендующий на особую интимность, не имел никакой опоры ни в киевском пантеоне, ни в фольклорных образах, известных восточным славянам".

Высказывается мнение, что "включение иранских богов в киевский пантеон было связано с попыткой Владимира привлечь на свою сторону хорезмийскую гвардию, приглашенную Хазарским каганатом в 70-х годах Х века. Роль хорезмийской прослойки киевского населения во введении этих божеств в киевский пантеон представляется историкам весьма правдоподобной. "Почитание сияющего Солнца и Симурга воинами-хорезмийцами киевского гарнизона было, видимо, ближайшей причиной появления Хорса и Семаргла в кругу древних киевских богов".

– Но кто же заставлял не киевских, а Владимирско–Суздальских князей изображать "малопонятного" Семаргла на стенах соборов и на главных воротах своих храмов… При этом бог Семаргл-Семиглав считался воплощением священного числа "семь" [32] от индоевропейского "седм".

Языковое сходство имен Симурга и Семаргла говорит не только об одновременности их существования в истории домонгольской Руси и очень древней истории Персии – Ирана, но и, возможно, о заимствовании очень древним (доахеменидским) Ираном имени славянского бога.

По гипотезе А.Т. Фоменко и Г.В. Носовского [6, стр.617], сама цифра "семь" была изобретена и получила свое название где-то в XV веке, как и остальные современные арабские цифры, на основе славянской скорописи… Возможно тогда же появились Семарглы и Симурги… О том, что в XV веке арабские цифры были не такими, как сейчас, известно, не только от Фоменко.

"Странные" цифры на картинах художников



Шюхлин. "Портрет супружеской пары". 1479 год. Знак тысячи обозначен римский буквой "М". Четверка и семерка далеки от обычных арабских цифр. [7]	Мастер 1477 года. "Голгофа". Фрагмент. Аугсбург. Тысяча обозначена "единичкой", четверка и семерка совсем не такие, как сейчас…[7]

"Мадонна с архангелом Михаилом и святым". Алтарная завеса. Германия. 1477. Эрмитаж. Странная дата…[8]
		Становление арабских цифр в Европе [9]

	Гравюра XVI века. "Птолемей и Астро-номия"
	[10]
	Шонгауэр. "Крестьяне, едущие на рынок". Вверху странная цифра. Если первая цифра - шестерка, тогда - это дата - 6979 год от сотворения мира или 1471 год НЭ. Шестерка явно "не настоящая" [39]



Шонгауэр. Девушка у огня. 1469 год [12]	Шонгауэр. Христос – судья страшного суда. 1469 год [12]


Шонгауэр. Сидящий мужчина [12]	Шонгауэр. Голова первосвященника [12]

На приводимых здесь иллюстрациях картин средневековых европейских художников даты подписаны "странными" цифрами. Семерка на них соответствует современной иранской восьмерке… В таблице из энциклопедии [9] приведены арабские цифры, в период их становления, в течение XV века. Сразу видно, что в середине XV века в Европе не было современной цифры "пять"! Вместо нее писали современную "четверку", а вместо "четверки" – рисовали бантик, как показано и на картинах эпохи Возрождения. На этих картинах показано, что вместо единицы в знаке тысяч могли написать римскую цифру-букву "М". У Дюрера на некоторых гравюрах XVI века цифра "пять" изображена задом наперед! У большинства немецких художников первой половины XVI века даты на картинах и рисунках записаны цифрами, которые значительно отличаются от современных.

То есть, в конце XV века современное написание арабских цифр еще не было достигнуто.

Еще один пример – фрагмент гравюры XVI века, где изображен античный Птолемей в средневековой короне и Астрономия [10. Стр. 82]. В руке у Птолемея сектор с небесными координатами, на котором цифры 2, 3, 4 выглядят, как сегодня, а вот цифра 5 нарисована наоборот, "шестерку" не видно, а "семерка" - тоже нарисована наоборот.

Вот четыре даты с рисунков Шонгауэра (1440-1491), которые датируют XV веком. Написание четверки разное, то по-итальянски близко к современному написанию (в дате 1470 года), то по-немецки (в дате 1486 года). В дате 1486 год восьмерка подправлена. В датах 1469 год – девятка выглядит, как знак вопроса.

Какими были цифра в эпоху Возрождения можно проверить по фотографиям старинных часов, созданных в XV веке. На башне часов в Венеции, построенной в 1485-95 годах, на циферблате указаны римские числа от I до XXIV. А на иллюстрации к "Истории Фридриха и Максимилиана", написанной Альтдорфером в 1510 году, показаны уже арабские цифры на циферблате часов [12]. Цифры 1, 2, 8, 9, 0 соответствуют сегодняшним. Но остальные цифры: 3, 4, 5, 6, 7 – явно не настоящие. Можно предположить, что сам циферблат был изготовлен раньше, чем была написана картина. Однако на датах, которые ставил Альтдорфер на своих картинах и рисунках уже в XVI веке, указаны эти же самые неправильные цифры. А, если учесть, что цифра, похожая на цифру 5, на самом деле является цифрой 6, возникает вопрос – даты из какого столетия записаны на произведениях искусства XVI века.


Кадусси, Ламбардо, Массари, Анкоре (скульптор). Венеция. Башня часов. 1485-95 [13]		Циферблат Башни часов в Венеции. Очень похожий циферблат есть на часах в Брешии, на севере Италии, на площади Лоджия.

Циферблат на часах замка.		Альтдорфер. "История Фридриха и Максимилиана". 1510 год [12]

Цифры 3 и 4	Цифры 5 (слева) и 6	Цифры 6 (слева), и 7	1512 год на рисунке Альтдорфера "Рыцарь и Ландскнехт" [12]



Шейфеляйн. Мальчик на коне. 1518 год [12]	Шейфеляйн (1485 – 1540). Всадник на коне. Считается, что 1507 год, потому что 1567 год не подходит…


Шейфеляйн. 1507 год [12]	Шейфеляйн. Святой Себастьян. 1519 год [12]

Ниже приведены даты с рисунков немецкого художника XVI века Шейфеляйна (1485 – 1540)

1507 год

1507 год?

Или 1567 год ???

1518 год

1519 год

или J519 год

Здесь "Пятерка" – не немецкая, а похожа на современную. Это подозрительно. Немецкие современники Шейфеляйна пятерку рисуют не так. Однако и у Шейфеляйна встречаются странные пятерки. Вот, например:


Шейфеляйн. Тайная вечеря. 1509 год. [13]	В 1507 году почти нормальная пятерка, а здесь не совсем нормальная…


Шейфеляйн. Анна с Марией и младенцем. 1511 год. [13]	Пятерка, похожая на тройку

Когда Фоменко и Носовский выводят наши "арабские" цифры из скорописи букв древнерусского алфавита, они сравнивают эти буквы уже с современными цифрами. Цифры на картинах итальянских художников конца XV века наиболее похожи на современные. А вот "Странные цифры" на картинах и рисунках немецких и голландских художников XV – XVI веков не подтверждают гипотезу о происхождении этих цифр из древнерусских букв.

Цифры, используемые в арабском мире и в Иране, тоже вряд ли произошли от древнерусских букв. Хотя, когда традиционные историки показывают пути, которыми шло становление цифр в Европе и на Востоке, на этих путях соседствуют и европейские, и иранские цифры.

В свете Новой хронологии было бы очень интересно рассмотреть вопрос о происхождении "восточных" – арабских и иранских цифр. Какими цифрами пользовались в Византии? Какими цифрами и символами оперировал Архимед при решении древнегреческих систем уравнений? Каким образом древневавилонскими клинышками решались задачи по предсказанию солнечных затмений? И какими цифрами пользовался средневековый и среднеазиатский Улугбек?

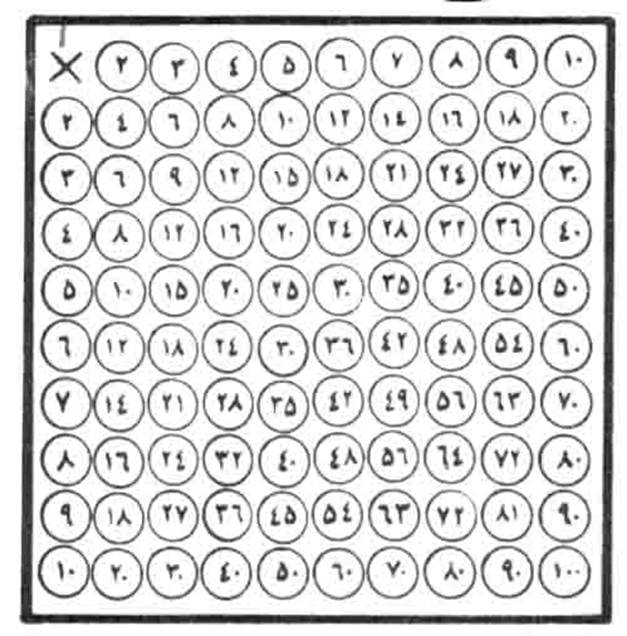
Современное написание арабских цифр в Иране показано на таблице умножения с обложки ученической тетради.

По-ирански "пять" - "пядшт", "шесть" - "шешт". Иногда в скорописи их двойка, тройка и четверка отдаленно похожи на наши, но повернутые вправо на 90 градусов.

Современные арабские (западные) цифры; Арабские буквы (использовавшиеся, как цифры); Современные арабские (восточные); Ранние арабские (восточные) [5]

Современные арабские (западные) цифры; Ранние Деванагари (Индийские); Поздние Деванагари [5]

Иранская таблица умножения. Порядок чисел соответствует европейскому – слева направо, сверху – вниз.

Здесь же некоторые общепринятые меры в иранском выражении.

Эволюция арабских цифр в средневековой Европе

Считается, что распространение в Европе арабских цифр началось в X веке из Испании, где переводились арабские трактаты по математике.

Каким образом происходила эволюция арабских цифр в средневековой Европе от X до XV века показывается в книге французского математика марокканского происхождения Дж. Ифрака "Универсальная история чисел" в переводе на немецкий (издание 1991 года). Таблицы из этой книге приведены в книге Е.Я. Габовича "История под знаком вопроса" [2].

Из таблиц видно, что все арабские цифры меняли свое написание в течение веков. Двойка временами была похожа на сегодняшнюю четверку, четверку можно было принять за восьмерку, пятерку спутать с четверкой. Рассмотренные в таблицах 47 рукописей не дают полный обзор вариантов в написании арабских цифр в средневековой Европе, но даже на основании этого материала Е.Я. Габович делает интересные выводы.

- цифра 1 еще в XIII веке могла приниматься за цифру 7, а в XV веке известно ее написание в виде знака вопроса, который можно интерпретировать как цифру 2,

- цифра 2 долгое время писалась вверх ногами и могла быть принята за цифру 6,

- цифра 3 иногда писалась, как сегодняшняя цифра 4, иногда, как сегодняшняя цифра 5,

- цифра 4 иногда писалась, как сегодняшняя цифра 5, а иногда в форме, едва отличимой от сегодняшней цифры 9,

- цифра 5 в течение многих веков писалась, как сегодняшняя цифра 4, иногда как сегодняшняя цифра 9 и изредка, как 7,

- цифра 6 иногда писалась, как сегодняшняя цифра 4, а иногда, как цифра 3, повернутая на 180 градусов вокруг вертикальной оси,

- цифра 7 иногда похожа на современную цифру 1, а иногда на 4,

- цифра 8 иногда писалась, как сегодняшняя цифра 9 или как 4,

- цифра 9 иногда можно спутать с цифрой 2, а иногда с запятой,

- цифру 0 можно спутать с шестеркой или с девяткой.

Не зная динамику написания арабских цифр в средневековых документах, историки XVII – XVIII веков могли неправильно интерпретировать найденные в этих документах цифры, а также неверно датировать сами древние документы. Метаморфозы цифр, возникающие в результате их вращения вокруг оси, могли происходить при использовании цифр по различному назначению. Например, цифры в дате, на рисунке или на картине, обычно изображаются в одну строку, "вверх головой", однако, эти же цифры на циферблатах часов изображались по-разному, чаще всего под углом к вертикали, в зависимости от конкретного часа, то есть цифры могли располагаться под углами ± 30, 60, 90, 120, 150 градусов, а также "вверх головой" в 12 часов и "вниз головой" в 6 часов. Таким образом в XV – XVI веках изображались и римские, и арабские цифры. Сегодня на циферблатах цифры обычно изображаются "вверх головой".

Становление в Европе арабских цифр (X – XIII века). Ноль отсутствует![3]

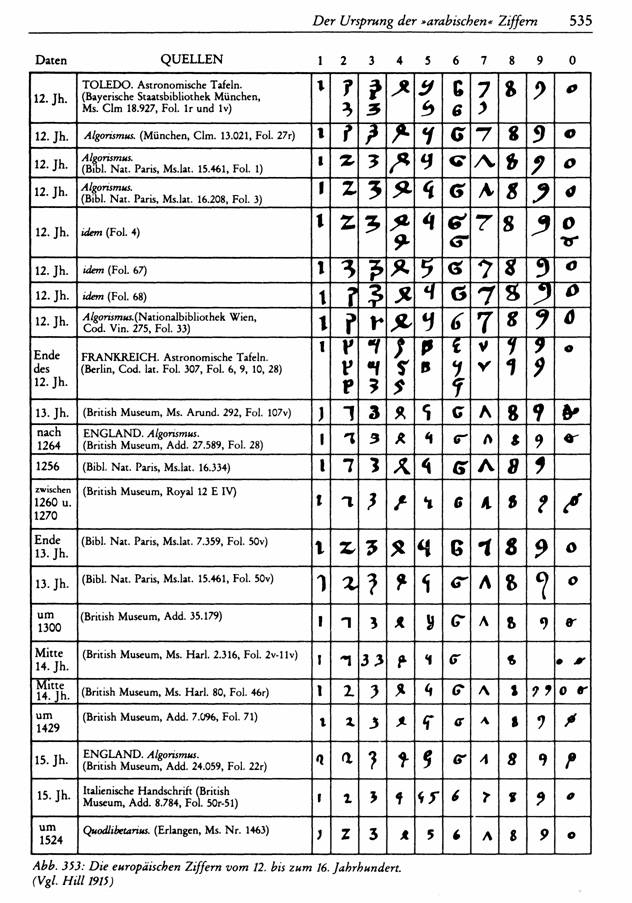
Становление в Европе арабских цифр (XII – XV века) [2, 3]

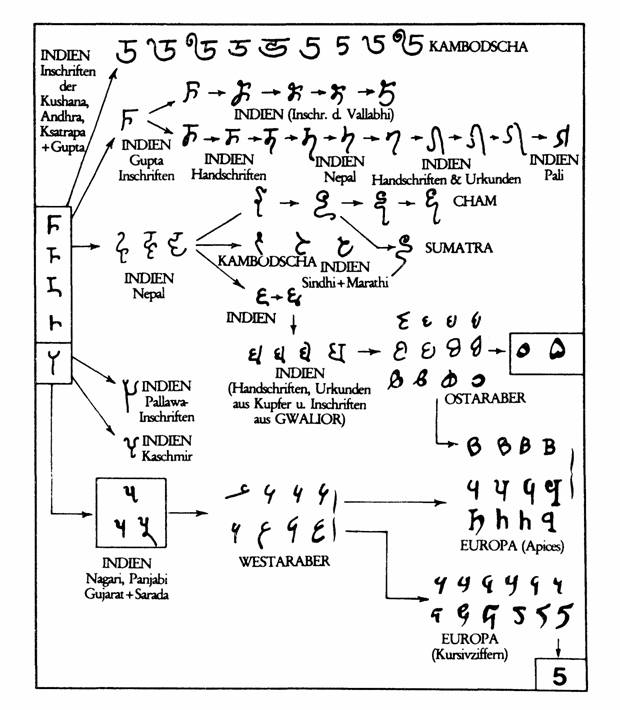
Метаморфозы цифры "пять" при продвижении из Индии в Европу [3]

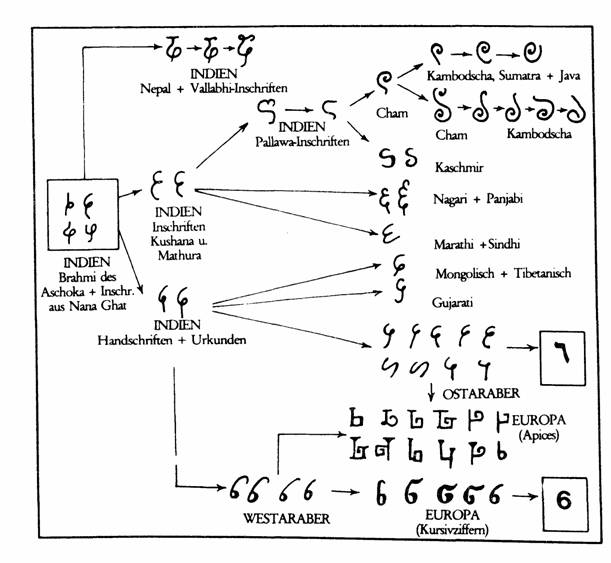
Метаморфозы цифры "шесть" при продвижении из Индии в Европу [3]

О системах счисления

Здесь несколько определений, связанных с цифрами, датами и системами счисления.

Система счисления — способ записи чисел с помощью заданного набора специальных знаков (цифр).

Непозиционная система счисления — система счисления, в которой вес цифры не зависит от ее положения.

Позиционная система счисления — система счисления, в которой вес цифры меняется с изменением положения цифры в числе и определяется написанием цифры и местом, которое она занимает.

Традиционная система счисления — позиционная система счисления, в которой запись числа состоит из двух частей — целой и дробной. Количество цифр перед разделяющей эти части запятой (точкой) заранее не известно и может быть сколь угодно большим. Фактически запись числа образует две последовательности цифр, разбегающиеся влево и вправо от запятой.

Единичная система счисления. Простейшая, но абсолютно неудобная система счисления. Основана на единственной цифре – единице (палочке). Позволяет записывать только натуральные числа. Чтобы представить число в этой системе счисления нужно записать столько палочек, каково само число. Использовалась нецивилизованными племенами, потребности которых в счете, как правило, не выходили за рамки первого десятка.

Вавилонская клинописная система счисления использовалась еще на заре человеческой цивилизации – в III тысячелетии до нашей эры. Она сочетала три основания – 1, 10 и 60. Для чисел от 1 до 9 использовались вертикальные клинья (палочки), как в единичной системе счисления. Для сокращения записи использовался угловой клин, заменявший 10 вертикальных. Угловой клин можно было повторять до 5 раз, а вместо 6 угловых клиньев вновь писался вертикальный, но перед ними. Тем самым наборы от 1 до 9 вертикальных и от 1 до 5 угловых клиньев превращались в цифры (десятичные и шестидесятеричные). Еще один специальный символ, аналог нуля, использовался для указания пропуска пустых разрядов, то есть для обозначения границы между шестидесятеричными классами, но лишь в тех случаях, когда без него запись числа могла бы стать двусмысленной.

Древневавилонские цифры и числа [14]

Шестидесятеричная система счисления. Ведет свою историю с Древнего Египта, то есть с IV тысячелетия до нашей эры. Ее появление вызвано сочетанием двух причин. Во-первых, при счете на пальцах можно фиксировать до 60 различных положений косточек или суставов между ними. Во-вторых, 60 лет – наименьшее общее кратное периодов обращения вокруг Солнца всех планет Солнечной системы, доступных для наблюдения без оптических приборов. Поэтому именно 60 лет были периодом, на который составлялись древние астрономические календари. Шестидесятилетний цикл летоисчисления широко известен как восточный календарь, в двух вариантах – японском и китайском. Шестидесятеричная система счисления до сих пор сохранилась в измерении углов и времени. Угол равностороннего треугольника делится на 60 градусов. Градус, как и час, делится на 60 минут, а минута – на 60 секунд. На шестидесятеричную систему счисления указывает и способ образования числительных от 60 до 79 во французском языке. Например, soixante-dix-nef (число 79) можно перевести как "шестьдесят и девятнадцать".

Египетские цифры [14]

Древнегреческая аттическая (вверху) и алфавитная (внизу) нумерация [14]

Деталь вазы персидского царя Дария изображает сборщика налогов, подсчитывающего налоги на счетной доске [14].

Дата – время. Традиционный способ представления моментов времени и промежутков времени сочетает использование нескольких разных единиц измерения. При переходе от тысячелетий к векам, от них к десятилетиям, а затем к годам, вес разряда в записи даты изменяется в 10 раз. Год состоит из 12 месяцев, месяц – из 4 недель, неделя – из 7 суток. Сутки состоят из 24 часов, час – из 60 минут, а минута – из 60 секунд. Более мелкие интервалы времени, чаще всего, измеряют десятыми, сотыми, тысячными долями секунды. Таким образом, здесь сочетаются системы счисления с шестью различными основаниями: 4, 7, 10, 12, 24 и 60.

Двенадцатеричная система счисления. На ее широкое использование в прошлом явно указывают названия числительных во многих языках, а также сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения. Год состоит из 12 месяцев, а половина суток состоит из 12 часов. В русском языке счет часто идет дюжинами. В английском языке есть особые, а не образованные по общему правилу, слова eleven (11) и twelve (12). Английский фунт состоит из 12 шиллингов.

Десятичная система счисления. Использует десять обычных цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы "+" и "–" для обозначения знака числа и запятую (точку) для разделения целой и дробной частей числа.

Римская система счисления. С помощью семи цифр – I=1 , V=5 , X=10 , L=50 , C=100 , D=500 , M=1000 – можно весьма успешно и довольно выразительно представлять натуральные числа в диапазоне до нескольких тысяч. Продолжает использоваться для указания порядковых числительных, часов, столетий, номеров съездов или конференций.

Ранее существовали греческая система счисления, похожая на римскую, но со своими символами для цифр.

Система счисления с основанием 40. Совершенно особое слово "сорок" и часто используемое в русском языке выражение "сорок сороков" явно указывают на употребление в прошлом и этой системы счисления.

Система счисления с основанием 7. Семь дней недели, семь нот, семь чудес Света, семь цветов радуги и другие примеры указывают на то, что и это число служило разрядной единицей. А название праздника "пятидесятница", как и пришедший из древнееврейского языка "юбилей" – это вовсе не половина от ста, а число, следующее за 49 – второй разрядной единицей системы счисления с основанием 7.

Славянская система счисления. Буквам старой славянской азбуки были присвоены цифровые значения: от 1 до 10, затем через 10 до 100 и через 100 до 1000.

Славянские цифры-буквы [14]

Пятеричная система произошла от счета на пальцах одной руки. Некоторые племена на филиппинских островах используют ее и в наши дни, а в цивилизованных странах ее реликт сохранился в виде школьной пятибалльной шкалы оценок. В [14] приводится пример использования непозиционной пятеричной системы счисления.

В сказке "Конёк-Горбунок", написанной П. П. Ершовым, есть примечательный эпизод. Царь, увидев златогривых коней и пожелав их заполучить, вступает с Иваном в торг.

Ну. я пару покупаю.

Продаешь, ты? — Нет, меняю.

Что в промен берешь добра? —

Два — пять шапок серебра. —

То есть это будет десять.

Царь тотчас велел отвесить...

Автор сказки хорошо знает тонкости русского языка, поэтому все слова им точно взвешены и употребляются к месту. Это, безусловно, относится и к непривычной для современного читателя форме обозначения десятка — "два — пять". Иван, не будучи большим грамотеем, торгуясь с царем, оперирует пятками, а более продвинутый в арифметике монарх переводит его примитивный счет в десятеричную систему. Но, если записать "два — пять" на бумаге, человек, не знакомый с пятеричной системой счисления, вполне мог бы прочесть это число как двадцать пять.

Традицию произносить числа без указания разрядов, а подразумевая их "по умолчанию", часто демонстрируют наши англоязычные современники, когда вместо "тысяча девятьсот девяносто" говорят "девятнадцать девяносто".

Автор статьи в журнале "Наука и жизнь" приводит эти примеры, чтобы подойти к такой интересной проблеме, как существенно преувеличенный возраст библейских персонажей. По его мнению причина тысячелетних сроков жизни Адама, Ноя, Мафусаила – неправильное перевод цифр при переходе от одной системы счисления к другой при переводе библейских текстов… Здесь важно, что речь идет об ошибках, появившихся при переводе или при переписывании уже записанного текста. Появление таких ошибок, сродни "верблюдам, проходящим сквозь игольное ушко", это пример того, что сам текст не сохранился в памяти в виде устного предания, передаваемого от одного поколения к следующему. Это касается не только библейских, но и любых текстов большого объема, таких, как поэмы Гомера, якобы передаваемых из уст в уста в течение нескольких веков перед тем, как их записали.

При обсуждении календарных проблем в средневековой Европе надо иметь ввиду, что эра "от рождества Христова" начинает упоминаться в документах с X века, однако первое известное обозначение даты "от рождества Христова" в документах римской папской канцелярии датируется 1431 годом [15].

Для описания дат в рисунках, гравюрах, картинах европейских художников следует иметь в виду, что даты "от рождества Христова" сокращенно обозначаются как A.D. (anno domini), A.D.I.X. (годы от рождения Иисуса Христа) или АХ, или только А. Даты от сотворения мира обозначаются "anno mundi".

Все это присказка. А впереди, непосредственно, произведения искусства и странные даты, запечатленные на них.




Титульный лист "Арифметики" Магницкого, 1703 год* [39]*	Фрагменты обложки "Арифметики" Магницкого.
Араб Архимед и испанский гранд Пифагор.	У Пифагора в руке свиток с нормальными арабскими цифрами.

А монеты в начале XVIII века (с 1701 по 1717 год) в России датировались буквами в датах от рождества Христова, в виде от АΨА =1701 до АΨЗI = 1717 [41]	Фотография копейки 1713 года (слева) и денги 1704 года [41]